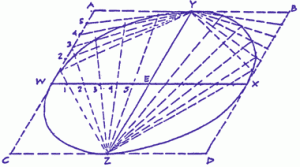
To draw a parallelogram ellipse given the conjugate diameters
 One of the subtlest of arcs is that of the ellipse. It has been extensively used in brick, stone and metal arch forms as well as in metal-work, ceramics and carpentry. The works of the great Baroque architect Borromini attest to the powerful visual impact of the ellipse. The method shown here explains how to practically develop the line of an ellipse which fits “inside” an angled parallelogram ,or rhombus.
One of the subtlest of arcs is that of the ellipse. It has been extensively used in brick, stone and metal arch forms as well as in metal-work, ceramics and carpentry. The works of the great Baroque architect Borromini attest to the powerful visual impact of the ellipse. The method shown here explains how to practically develop the line of an ellipse which fits “inside” an angled parallelogram ,or rhombus.
- Draw a parallelogram, with sides parallel to the conjugate diameters.
- Divide AW, WE into the same number of equal parts.
- Draw lines through points on AW to Y and through points on WE to Z.
- Produce lines through points on WE to intersect lines from AW. The points of intersection lie on the required ellipse.
- Join the points, repeat process for each quadrant of the parallelogram.
Masons, architects, carpenters, metal crafts workers and ceramicists will find this method extremely useful. It is absolutely accurate and rapid and eliminates the use of guess-work with the attached possibility of mistakes and awkwardness. Because the ellipse is “derived” methodically it can be repeatedly reproduced exactly the same without any confusion.