To inscribe a regular pentagon in a given circle (Euclid IV.11)
 The regular pentagon is one of the basic shapes in the vocabulary of design. The pentagon encompasses the Golden Section ,or Phi Ratio, and because of that it has held great symbolic impact for many civilizations throughout the ages. Medieval European and Muslim architects and designers included the pentagon and it’s derivatives in countless works. The method shown here uses the Golden Section Triangle ( the construction of which is given on another data sheet of the Handbook . This method avoids the inevitable inaccuracy which results from using a protractor to find the pentagon’s angles.
The regular pentagon is one of the basic shapes in the vocabulary of design. The pentagon encompasses the Golden Section ,or Phi Ratio, and because of that it has held great symbolic impact for many civilizations throughout the ages. Medieval European and Muslim architects and designers included the pentagon and it’s derivatives in countless works. The method shown here uses the Golden Section Triangle ( the construction of which is given on another data sheet of the Handbook . This method avoids the inevitable inaccuracy which results from using a protractor to find the pentagon’s angles.
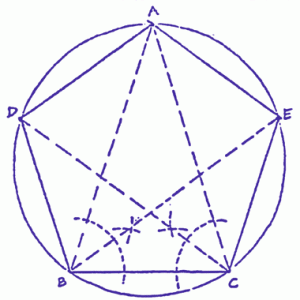
- Draw the circle about point O (center).
- Select a point (A) on the circumference.
- Construct a golden section triangle with its apex at A to fit inside the circle. (Use any golden section or phi triangle and make the angles of the triangle in the circle equal to those of that triangle).
- Locate points B and C on the circumference of the circle at the base of the inscribe triangle.
- Bisect angle ABC and angle ACB respectively.
- Produce the bisectors to intersect the circle at points E and D respectively.
- Connect points A, B, C, D, E to construct the inscribed pentagon.
There are endless patterns derived from the pentagon. Fabric designers, wood-carvers, quilters, and stained-glass workers will appreciate the practical utility of this method of drawing a pentagon. And, as did their predecessors over the ages, architects and landscape architects using this construction will be able to derive designs based upon the fascinating geometry of the pentagon.